

The basic aerodynamic aspect of the liftoplane is the choice of some airfoil for the wings of the rotor with obtaining the aerodynamic section coefficients of this airfoil for the relevant range of Reynolds numbers. Usually for such a task for any conventional aircraft it is enough to have only three kinds of such coefficients: of lift CL, of drag CD, and of moment CM, where the last, for much of aircrafts, uses 0.25 of the chord length as its referencing origin point. For the rotor of the liftoplane, the presence of such CM coefficients isn't enough. At first, I want to use not only a symmetric profile, but also an asymmetric one, which can provide some performance advantage. Such a profile also has the steady moment behavior with respect to 0.25 chord lengths. But its value is too high for steering the wing by gears, comparing with the moment of symmetric airfoil, which is near to zero. Thus, the position of the pivot for this should be optimized by moving it more in the trailing edge direction, as it pictured on the kinematic scheme of the rotor. So, having the CM values for some particular origin point isn't enough, since this optimization can be changed. And so, instead of having a particular CM, it is better to have the coordinates of the center of the entire aerodynamic force, from which the CM for any particular pivot position can be simply calculated. I call such coordinates: airfoil aerodynamic aggregations CFx and CFy for the X and Y coordinates of the center of force, respectively.
Also, this is still not enough. The wings of the presented rotor operate always in the prolate mode. And at the beginning of the acceleration of the aircraft on the runway, its winding ratio WR is higher than 1. It leads to AoAs of more than 90° for particular wings, but at a lower speed, when the drag is moderate. So, I need the aerodynamic coefficients and aggregations for the entire 360° range of possible AoAs, for enough freedom. Also, the range of airspeed values over all operations is very wide. But Mach number can be ignored for a relatively low-speed aircraft. So, finally, there needs a set of four coefficients and aggregations for the entire 360° range of AoAs in a wide range of Reynolds numbers. Therefore, I prepared such a set of aerodynamic data for the NACA 4410 airfoil in a form friendly for the simulation, using a composition of data from multiple sources, such as: XFOIL paneled simulation, CFD modeling for viscid and inviscid flow, and refactoring the public data of wind tunnel testing. This data has some degree of uncertainty, but this cannot affect the result of the entire simulation at a significant level. Examples of a distribution of the CL, CD, CFx and CFy over the entire 360° angles of attack for the Reynolds number 500,000, which were used in the flight dynamics simulation, are represented in the plots below.
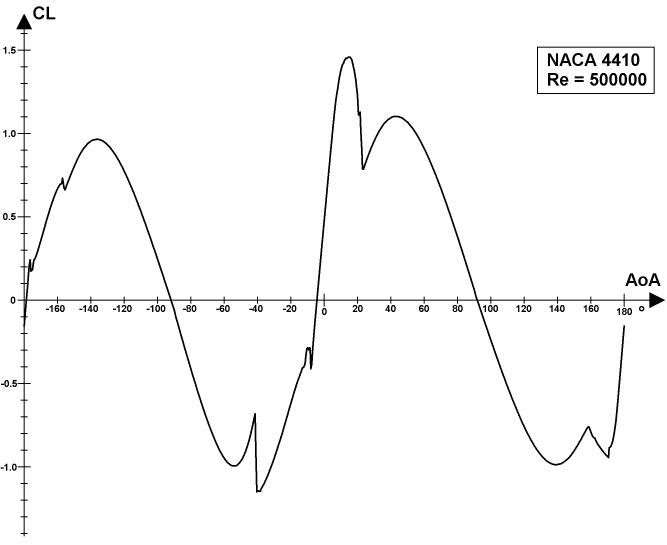
The plot above represents the distribution of the lift coefficients of the NACA 4410 airfoil over the entire 360° range of angles of attack for the Reynolds number 500000.
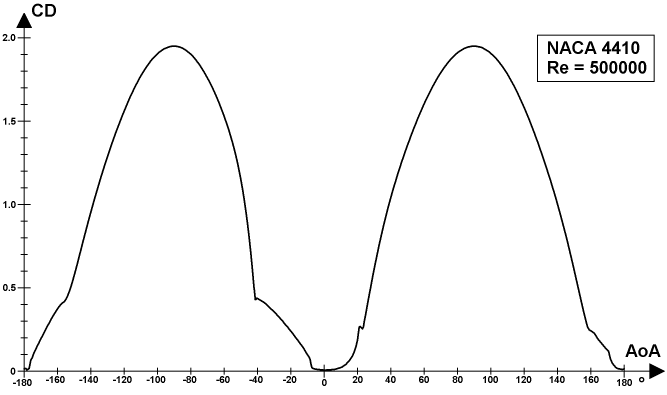
The plot above represents the distribution of the drag coefficients of the NACA 4410 airfoil over the entire 360° range of angles of attack for the Reynolds number 500000.
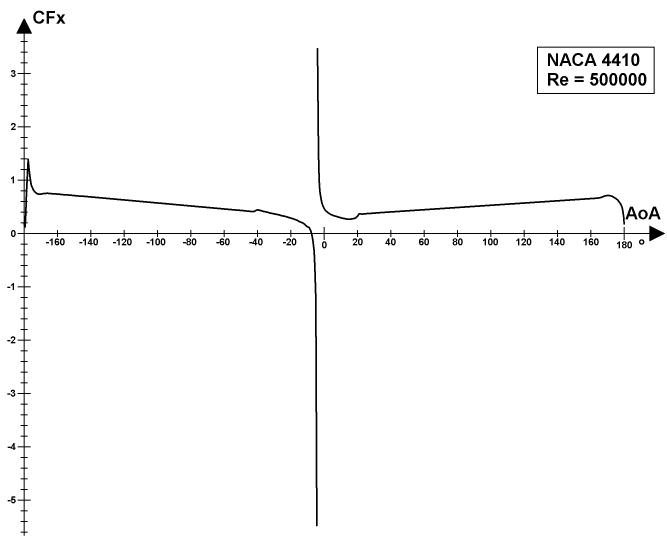
The plot above represents the distribution of the X-coordinate of the center of the aerodynamic force for the NACA 4410 airfoil over the entire 360° range of angles of attack for the Reynolds number 500000.
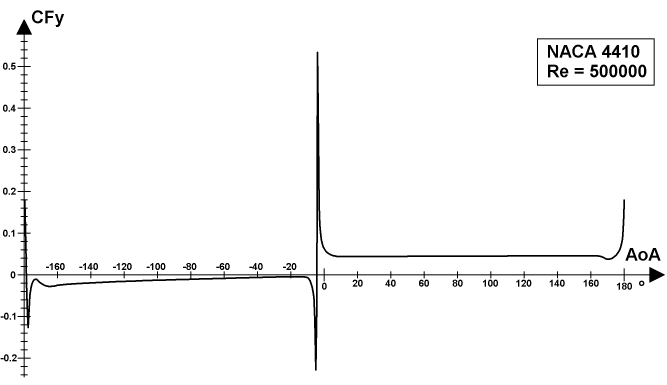
The plot above represents the distribution of the Y-coordinate of the center of the aerodynamic force for the NACA 4410 airfoil over the entire 360° range of angles of attack for the Reynolds number 500000.
Copyright © 2018-2023 Yuri Feldman - All Rights Reserved