

Principal aspects of the liftoplane were originated from the following thought experiment, which I imagined one day.
Consider an elevator (or lift), which is going up on some wire that is winding in a drum of this elevator by a power of its own engine. And now also consider that the other end of this wire is fixedly connected to some wing or lightweight glider that is gliding down. Also consider that the horizontal components of the speeds of both the elevator and the glider are equal, as well as the movement of both without acceleration. Additionally, suppose that the aerodynamic drag of the elevator and the wire is negligible. So this system will be in the presented movement while exists a free length of the wire. But for now, let's stay away from the problem of limited time of the movement and look at the instantaneous characteristics of this system.
The system has a certain center of gravity (CG), which moves forward at the same horizontal speed as both components of this system, and will move up if the elevator is going up at a speed exceeding the vertical speed of the glider that glides down. And so a potential energy of the entire system will increase due to a work performed by the engine of the elevator. Now the system can be considered, from the point of view the increasing energy, as if it were a some aircraft in the ascent, where the powering is at 100 percent mechanical. But such assumption may not be sound well for some people familiar with the realm of aircraft. Indeed, we know, a powered aircraft should have a something for the propulsion it forward, like a propeller, a turbojet engine or a rotor of a helicopter handled for the forward flight. On the other hand, it will not sound such surprisingly for people more familiar with the aspects of non-powered flight, for example for people with experience in sailplanes flying, hang gliding or paragliding. They know that any non-powered glider is propelled forward by gravitational force using energy from decreasing its altitude. More than, they have experience ascending in the rising air of a dynamic or thermal nature. This rising air acts as the elevator in the considered thought experiment in a purely mechanical way. And when the glider is going up in the rising air, it still continues to glide down relative to the air itself under the propulsive force of gravity, having a certain gliding angle. Also, such people know how to switch the direction of this propulsive force to decelerate the glider upon landing.
So, the considered system possesses some equivalence with a glider placed into rising air, and the power of the elevator acts there as the power of this rising air. And now we can find that the system possesses a powered lift instead of the powered propulsion of an airplane. And the gravitational propulsive component of the system is powered by increasing the altitude of the CG from the lift power. Also, we can find that a correct particular implementation of such an abstract concept of a "flying elevator" will have a great advantage over a conventional airplane. It is a very high propulsion efficiency, since the powered propulsion will be excluded from the scope of such a system as much as possible with a related loss of power in it.
Now, before going forward, let's look at the diagram below, which explains this concept in detail. There and elsewhere, I use the arrow sign to denote a vector. Also, I use the "^" sign to denote a normalized vector, i.e. a vector of unit length, the dot-product of which on some other vector is simply a projection scale of one vector onto the direction of the other.
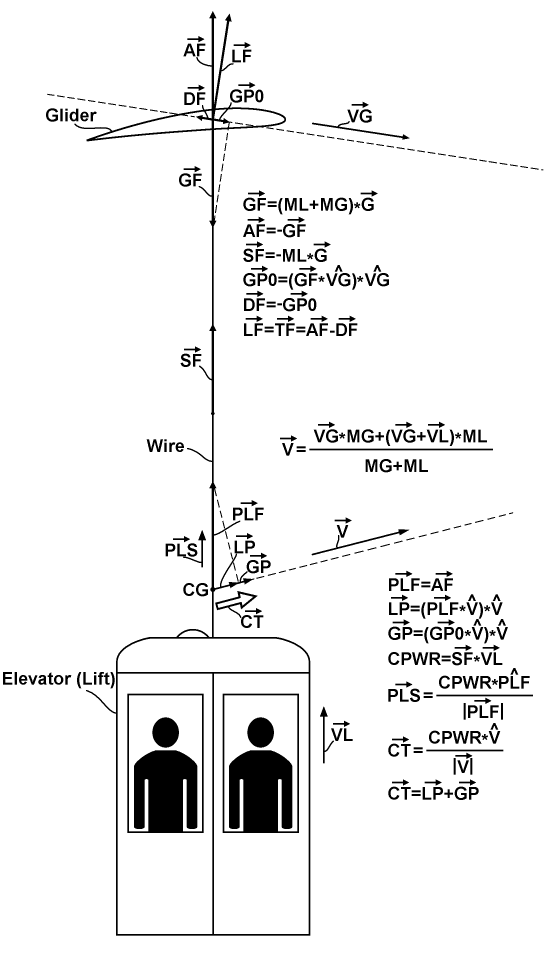
There the glider is connected by the wire with the elevator. The glider has a speed vector VG and undergoes a gravitational force GF, the value of which is formulated in the first upper equation, where the vector G is gravitational acceleration, and the masses of the elevator and the glider are denoted as ML and MG, respectively. The gravitational force GF is fully compensated by a full aerodynamic force AF, as it formulated by the second upper equation. The third equation represents a strain force of the wire SF, which is the opposite of a gravitational force of the elevator only. The aerodynamic force can be decomposed into two components: a component perpendicular to the airflow direction, which is a lifting force LF; and a component in the direction opposed to a source of airflow, which is a drag force DF. The gravitational force GF has a projection GP0 on the gliding direction, the value of which is formulated in the fourth upper equation. The GP0 force exactly compensates for the drag force DF, and so it acts as a propulsive force, as it is reflected in the fifth equation. I will reference the GP0 force as a primary gravitic propulsion force. The sixth upper equation represents another side of the using the lifting force LF as a thrust force TF, which is applicable in the realm of helicopter aircraft and also in some explanations of the presented invention. And this equation presents a simple way to calculate it by subtracting the drag force from the full aerodynamic force, vectorially.
The full speed of the elevator is simply the algebraic vectorial sum of the gliding vector VG and a winding lifting speed vector VL. The CG point on the wire represents the center of gravity of the entire system itself. This point has its own speed vector V, the value of which is formulated by the weighting equation in the center of the diagram. In the current example the CG point is placed on the wire, but in more complex cases, it can simply be placed in space. And so, it isn't attributed to a some element of the system, it is attributed to the entire system. The CG point possesses the mass of the entire system, so the balance of the AF force and the GF force can also be considered there. But the AF force is referenced there by another name as a power lifting force PLF, which means that the CG point is a subject of some lifting. It is reflected in the first equation of the lower group. We will encounter a duality of actuation of the lifting force PLF by projecting it onto the vector V. It brings a lift-propulsion LP, which is represented in the second equation. Also, a projection of the primary gravitic propulsion GP0 onto the vector V brings an entire gravitic propulsion GP, which is represented in the third lower equation. The fourth equation represents a consumed power CPWR as the dot-product of the strain force SF on the elevator's winding speed VL. Having this power, we can calculate two vectors. The first is a power lifting speed PLS, which is represented in the fifth equation. And the second is a consumed thrust CT, which is represented in the sixth equation. Also, we can see that the sum of the both kinds of the propulsion is equal to the consumed thrust, as it is represented in the seventh equation. These PLS and CT represent a duality of powering the system. For the first we can say as presence a lift powering, but for the second we can say as presence a thrust or propulsion powering. But we should understand that they are connected by the common power value CPWR, which is a scalar quantity, and so, it doesn't represent a particular force doing the work. There is simply an exchange of the power between the elevator and the gravity field by increasing or compensating the altitude of the CG.
Let us now look at a particular case where the CG has only horizontal movement. It will be corresponded to an aircraft on a cruise. The LP for this case is equal to zero. And the system goes forward only by the gravitic propulsion GP, but a power for this propulsion is provided by the elevator. In this case the absolute propulsion efficiency will be defined by a loss of the moment of airstream through a downwash of the glider. But this loss is already included in the balance of the entire drag as induced drag. However, the direction of the entire drag is not exactly parallel to the horizontal flight path direction of the CG, leading to the existence of a small projection of the small downwash onto this flight path, and consequently to existence a very small remained loss, which is less than 1 percent, actually. So, the propulsion efficiency relative to the non-powered wing will be more than 99 percent.
Let us now look at the case when the elevator is not working. It will be simply a gliding. The LP will be exactly compensated by the GP and so the CT will be equal to zero in the full accordance with the non-powered flight.
There is also another interesting variant of applying of the "flying elevator" concept, now for the analysis of the induced drag itself during gliding. From the lifting line theory, it is known that the induced drag is created by a vortex associated with the wings of the finite span. It is known as a "horseshoe" vortex. This vortex creates some complex induced deviation of the base flow. This component, at the near infinity in the downstream direction has a vertical direction and is known as downwash. Also, this component in the vicinity of the wings themselves is known as inwash or inflow. This inflow also points down in the in the direction opposite to the lift force, but it is half as much as the downwash. Since this component represents a loss, it is mapped for practical use to those induced drag by a reposition of the actual aerodynamic force to the reference frame of the non-disturbed stream in far infinity. But on the other hand, it can be considered as a kind of a permanent sinking air. This sinking air can be considered as a negative powering, where the potential energy is going back to a power source. But the power source there is the gravity field itself, which provides the propulsion to compensate for the airfoil section drag. But the powering of the "horseshoe" vortex also needs an energy. And so, we can see that the gravity power there is split in two ways. The first is simply compensation for the airfoil section drag, such as profile drag. And the second is the powering of the "horseshoe" vortex that performs a self servicing for this powering by placing the glider inside of the sinking air of the inflow. It looks interesting, but what a useful thing can be extracted from that? It is horizontal acceleration. The horizontal acceleration of the glider will be powered only by the first component that is the gravitic propulsion, since the "horseshoe" vortex stole the second for its own servicing. For using this feature we should consider a gliding of the glider inside its own inflow. For such a gliding a corresponding gliding angle exists. It can be referenced as a local gliding angle (LGA) of the glider. Now consider, we have some implementation of the "flying elevator" concept in a some aircraft. A particular flight of such an aircraft can be decomposed to a "glider" component and a "lift" component. Let's name the "glider" component as embedded virtual glider or simply a virtual glider. So, said LGA can be obtained from this virtual glider. Knowing this is useful for understanding when the aircraft will accelerate or decelerate for any particular flight operation. A real glider cannot instantly change its LGA to correct its acceleration, since such a change is linked to a change in the flight path stabilized by the entire mass of the glider. But the virtual glider can do this simply by changing a handling of its actuator.
Another interesting thing that this concept can provide is the ability for a recuperation energy with the same level of efficiency as spending it on the flight. To do this, we only need to switch the direction of the winding lift speed, and the aircraft will enter in a recuperative descent. More than, the "glider" can simply exchange an exceptional speed to an additional altitude, and that altitude can be wound back for gaining energy. Doing both of these actions at the same time, we can perform a recuperative deceleration too.
Now let's look how the "flying elevator" concept applies to the known types of aircraft. Let's look on an airplane on a cruise flight. The airplane will have zero flight path angle due the cruise operation. And so, the projection of the gravitational force onto the drag direction is also zero, which disables the actuation of the gravitic propulsion. The airplane compensates for the drag using a separate actuator, such as a propeller, turbojet or turbofan engine. The separate actuator has a significantly smaller thrust specific area than the wings of the airplane. From the lifting line theory, it is known that the thrust specific area of the wings themselves, which create the downwash, is almost equal to the area of the circle which diameter is based on the wingspan. The separate actuator of the airplane has a high outflow speed, which limits its propulsion efficiency. For the propeller, this efficiency practically lies in the range of 0.5 - 0.8. Also, the propellers perform badly at speeds close to subsonic. The turbojet engines perform well at the subsonic speeds, but their propulsion efficiency lies in the range of 0.2 - 0.3. The turbofan engines in the subsonic flight have a propulsion efficiency of the fan itself about 0.7, for the nozzle - only about 0.25, and the overall - about 0.5. But the low nozzle propulsion efficiency is partially compensated by a high thermal efficiency of the nozzle stage itself, which is about 0.65. So, its overall efficiency relative to fuel energy is about 0.37. Now we can see that having the propulsion efficiency near to 100 percent can elevate the overall efficiency up to 0.4-0.45.
Next we can analyze an autogiro on cruise. Projection of the gravitational force onto the plane of the blades of its rotor is not equal zero. But, nevertheless, it performs as a wing of an airplane, having a complete zero effect of the gravitational force on the movement of the blades, and a separated additional actuator is also used there for propulsion.
Let's now look at a helicopter in a cruise flight. There is a different picture. Its rotor is actuated on such manner that the blades are in a flapping motion over the entire turn. Their wingtips lie on a common surface inclined at an angle toward the direction of flight. So, a part of the entire thrust is horizontal and performs horizontal propulsion. But, we can see a difference in the gliding of the blades at different phases of rotation. A wing begins gliding down toward the direction of flight. It undergoes a gravitic propulsion with an increased magnitude of aerodynamic force. And the helicopter itself is going up like an elevator powered by the engine of its rotor. After that, the direction is switched, and the wing is flaring up with a decreased magnitude of aerodynamic force. And the helicopter is going down like an elevator with reduced power consumption. The difference in the powering for both of the considered phases, based on the vertical component of the rotor's thrust, can be considered as a lifting with a PLS compensating for the sink rate of the embedded glider during the gravitic propulsion. Also, for the duality of representation, we can consider the horizontal component of the entire thrust as the consumed thrust - CT. And a core feature of a helicopter, which permits that, is the common actuation area for those actions, due to using its rotor as a common actuator. So, a helicopter is kind of aircraft, which can be referenced as self-actuating aircraft (SAA), because it does not need a separate actuator for the propulsion. It uses for that the same actuator as for providing the sustaining forces. Thus, the propulsion feature of such aircraft has a large thrust specific area, low outflow and high propulsion efficiency.
Now we can see that a helicopter is an example of the SAA aircraft, which reflects the "flying elevator" concept in its operation. But a helicopter isn't an optimal implementation of this concept, because it was designed for a different target. It was designed for vertical flight in the first order and for horizontal flight in the second. But the concept itself was formulated to design an aircraft with the ideal propulsion for cruise flight. And a particular drawback of the helicopter in the implementation of this concept is the weak gliding ability of its rotor.
After understanding the existence of the SAA aircraft, we can look for other examples of this kind. I suppose, it can be understood that the birds' flight is an example of this kind. Indeed, the birds have only one actuator for both sustain and propulsion actions - their wings. Also, some birds can reach very high speeds in horizontal flight. It is the gravitic propulsion of a simple glider, which allows that. They can never reach that only by a flapping their wings in a weightlessness environment. They use this flapping mainly to lift themselves, compensating for the glide-sinking rate. There were attempts to build ornithopters that mimic the birds' flight. But I suppose that the trend isn't correct. The birds' flight has a big drawback for using it for people. This is a high level of the oscillated acceleration, mainly in the vertical direction. Birds are well accustomed to it, but it would be a variant of an uncomfortable flight for humans.
Copyright © 2018-2023 Yuri Feldman - All Rights Reserved